Nach 26 Jahren der Abstinenz fand in unserem Verein wieder ein Turniersimultan-Wettkampf statt. Es fanden sich sieben Freiwillige, was gerade noch in einem Durchgang zu bewerkstelligen ist. Wie schon der junge Carl Friedrich Gauß wusste, berechnet sich die Anzahl der Partien wie folgt:
(n * n – 1) / 2
Das ergibt bei n = 7: 21 Partien. 21 Bretter, Figurensätze und Uhren wurden herangeholt und auf zwei Tischreihen á 12 und 9 verteilt. Dann wurde für jeden Teilnehmer eine eigene Farbe ausgelost, die an den Tischen die eigenen Partien kennzeichneten. Weiß der Himmel, wie Matze die Verteilung jeder gegen jeden aus dem Kopf hinbekommen hat. Einziger Kritikpunkt: er hatte sich selbst 4 Schwarz- und nur 2 Weißpartien zugeschanzt. Alle anderen waren offensichtlich zufrieden.
Gespielt wurde mit einer Bedenkzeit von einer Stunde. Das hört sich erstmal nach viel an, schrumpfte aber gewaltig angesichts der lange Wege, die man zwischen den eigenen Brettern zurückzulegen hatte. Der Berichterstatter hatte beispielsweise 4 Partien auf der kurzen Reihe und 2 auf der langen. Und genau diese beiden Partien verlor er auf Zeit. Klar, die Partien auf der langen Gerade kamen eindeutig zu kurz. Aber auch wenn einige Partien durch dumme Flüchtigkeitsfehler (zum Nachdenken fehlte die Zeit) verloren wurden, hat es doch Spaß gemacht.
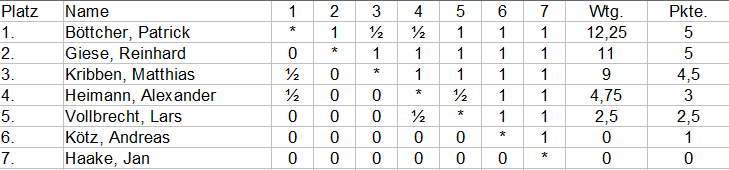


Es hat enorm Spaß gemacht und schreit dringend nach einer Wiederholung! Als ich Alexander mit einer Minute auf seiner Uhr in einem totremisen Ungleiche-Läufer-Endspiel Remis anbot, kollidierte mein Fairnessgefühl anscheinend mit den Benimmregeln in dieser Variante – alle anderen haben ihre Zeitvorteile voll ausgenutzt. Der arme Alex hatte die letzten 4 Partien simultan zu bestreiten, während seine Gegner am Brett stehen bleiben konnten. Der Trick scheint zu sein, rechtzeitig 1-2 Partien zu beenden und damit am besten noch die Laufwege abzukürzen…
Am 29.ten August besteht die nächste Möglichkeit, wenn sich nicht alle im Urlaub befinden.
Nur eine späte wenn auch vielleicht nicht unwesentliche Anmerkung, weil jetzt mittels Google Turniersimultan-Suche bei Schach in Spandau gelandet:
Der junge Carl Friedrich Gauß hätte gleich gewusst, dass mittels obiger Formel (n * n – 1) / 2 und mathematisch korrekter Ausführung die Anzahl der Partien FALSCH berechnet worden wäre, nämlich bei n=7 dann 24 und nicht 21 ! Bekanntlich geht ja Punkt- (also Multiplikation) vor Strichrechnung (Plus bzw. Minus), d.h. nach obiger Formel muss zuerst n*n gerechnet werden, dann 1 abziehen und zuletzt durch 2 teilen: also (49-1)/2 = 24.
Glücklicherweise wusste der junge Carl Friedrich Gauß besser, wo die Klammer richtig hingehört, um dann als richtiges Ergebnis auch 21 zu erhalten; nämlich so: n * (n – 1) / 2
Mathematik und Schach haben ja viel gemein, und der obige Regelverstoß ist vielleicht schachlich vergleichbar wie bei der Rochade zuerst denn Turm statt König zu ziehen. Kleine aber doch feine Unterschiede, die beachtet werde sollten.
Na ja, sinngemäß wurde die Formel richtig erfasst, denn das Ergebnis war ja korrekt. Es handelt sich also weniger um ein Verständnisproblem als vielmehr um einen Tippfehler.
Dennoch: gut aufgepasst!